Localisation de robots

Cette page est une ancienne page de mon site, je m'excuse pour son graphisme non cohérent par rapport au graphisme du reste du site. Cependant, je pense que tout y est bien lisible.

Définition d'un problème de localisation

Méthode angulaire par barycentre

Présentation du problème :

Faisons simple pour commencer. Supposons un cas en 2D avec trois stations $B_i$ de références aux positions dans $\mathcal{G}$ connues. Ces trois stations sont observables par le robot visuellement (elles sont peut-être reconnues soit par vision classique, soit elles émettent un rayonnement infrarouge par exemple) et sont discernables entre elles. En d'autre termes le robot les voit et sait affecter une position à chacune dans le référentiel global  $\mathcal{G}$.
Si de plus, R connait son cap (c'est à dire son orientation par rapport au référentiel  $\mathcal{G}$) grâce par exemple à un magnétomètre, alors, il est capable de déterminer les anges entre les  $B_i$ et l'axe x du référentiel   $\mathcal{G}$ .
Donc on note $\theta_i = (\vec{x}_\mathcal{G} , \vec{B_iR})$ cet angle. Avec les trois angles correspondant à chacune des stations on est capable de trianguler le robot et d'estimer sa position.

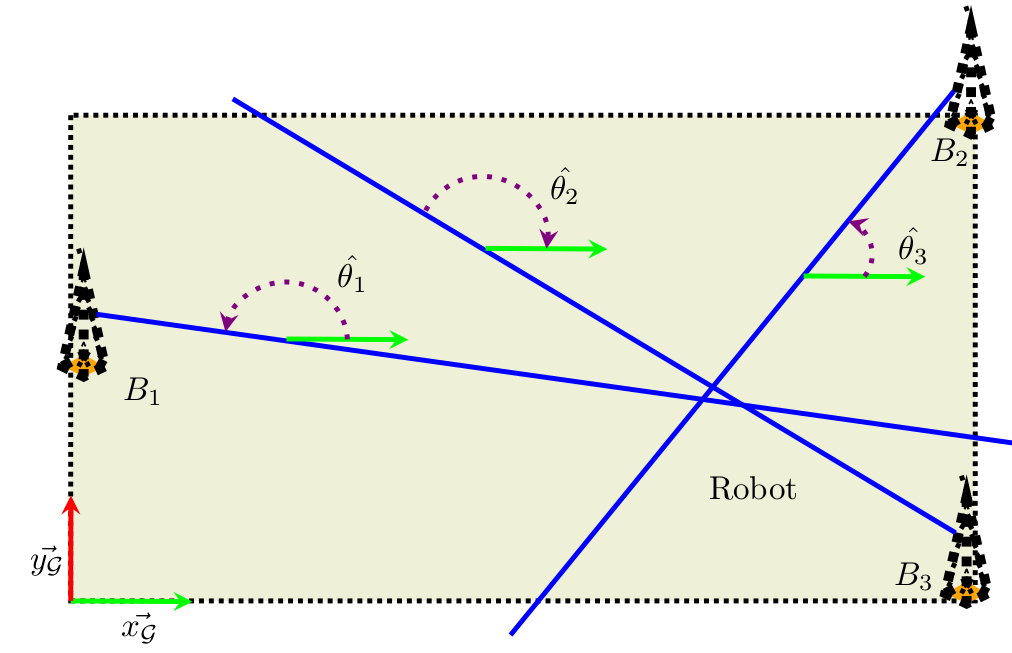
Figure : Illustration du dispositif; Erratum : les angles ont bien sûr la même convention d'orientation, à vous de choisir!
Modèle de mesure
On supposera que l'angle  θi estimé par le robot est entaché de bruit additif gaussien et centré. On admettra que l'estimation de l'angle suit la loi stochastique suivante : $$\hat{\theta_i} = \theta_i + \nu \text{ avec } \nu \sim \mathcal{N}(0,\sigma^2).$$Ce terme $\nu$ nu d'erreur d'estimation est homogène à un angle et dire que sa variance est constante est une approximation un peu grossière puisque l'erreur angulaire dépend de la distance à laquelle se trouve le robot de la balise. Ce modèle n'est donc valide que si l'on se situe à proximité des balises et dépend de la méthode de mesure des angles en elle même. Cet exemple étant introductif, nous ne rentrerons pas dans ces détails.

Obtention des points d'intersection : quelques considérations géométriques

Notre objectif est d'estimer là où se situe le robot. On peut penser, au vu du titre de cette section, et à juste titre que choisir le point moyen (l'isobarycentre) des intersections des droites paramétrés par les angles $\hat{\theta_i}$ mesurés par le robot et passant par chacune des stations de bases aux positions connues.
On peut appliquer la méthode suivante :

• Détermination des équations de droites en coordonnées cartésiennes dans le référentiel global pour chacune des stations de base
• Chaque point appartenant à une droite respecte la relation :$$y = mx + p \text{ avec } m,p \in \mathbb{R}.$$
• On peut trouver le coefficient directeur m par sa définition trigonométrique (la pente de la droite étant directement liée à $\hat{\theta_i}$ )$$m = \frac{dy}{dx} = \tan (\theta_i).$$
• Ensuite trouver p est facile avec les coordonnées du point Bi : $$p = y (B_i) - m x (B_i).$$
• Détermination des intersections
• On initialise N = 3 (trois intersections a priori)
  
• Si les deux droites sont quasiment alignées, il ne faut pas rechercher leur points d'intersections car ces derniers pourraient bien se situer en dehors des limites du terrain dans lequel évolue le robot. Ainsi, pour deux droites $D_i$  et $D_$ on peut calculer la différence de leur coefficients directeurs et ainsi faire le test : $$|m_i-m_j|<\epsilon, \epsilon \in \mathbb{R}.$$
• Si le test est un succès alors les droites sont quasiment parraléles on ne calcule pas leur intersection on fait N = N -1 et on passe à la droite suivante si il en reste.
• Sinon, on garde N inchangé et on peut calculer l'intersection par :$$\begin{cases} x_{intersection}^k = \frac{p_j - p_i}{m_i-m_j} \\ y_{intersection}^k = x_{intersection}^k m_i + p_i \\ \end{cases}$$
• Estimation de la position du robot : On calcule donc l'isobarycentre (moyenne) des positions et on obtient une position estimée du robot : $$\hat{\mathbf p}_\mathcal{G} = \begin{bmatrix} \hat{x} \\ \hat{y} \end{bmatrix} _\mathcal{G} = \frac{1}{N}\sum _{k=1}^N \begin{bmatrix} x^k_{intersection}\\ y^k_{intersection} \end{bmatrix}.$$Et voilà nous obtenons un estimé de position avec seulement des outils d'enseignement secondaire. Un petit essai s'impose en Python.
  

Un script d'essai en Python (open source) et quelques résultats.
Voici un code démonstratif avec un générateur de trajectoire de robot aléatoire. On notera qu'il faut installer python pour le faire fonctionner ainsi que les bibliothèques pyplot (pour les graphiques) et numpy (pour les notions algébriques). On règle le bruit fait sur l'estimation des angles à $\sigma = 2 \degree$  .

Voici les résultats pour des trajectoires situées dans la zone de jeu (symbolisées par le rectangle en pointillés) :

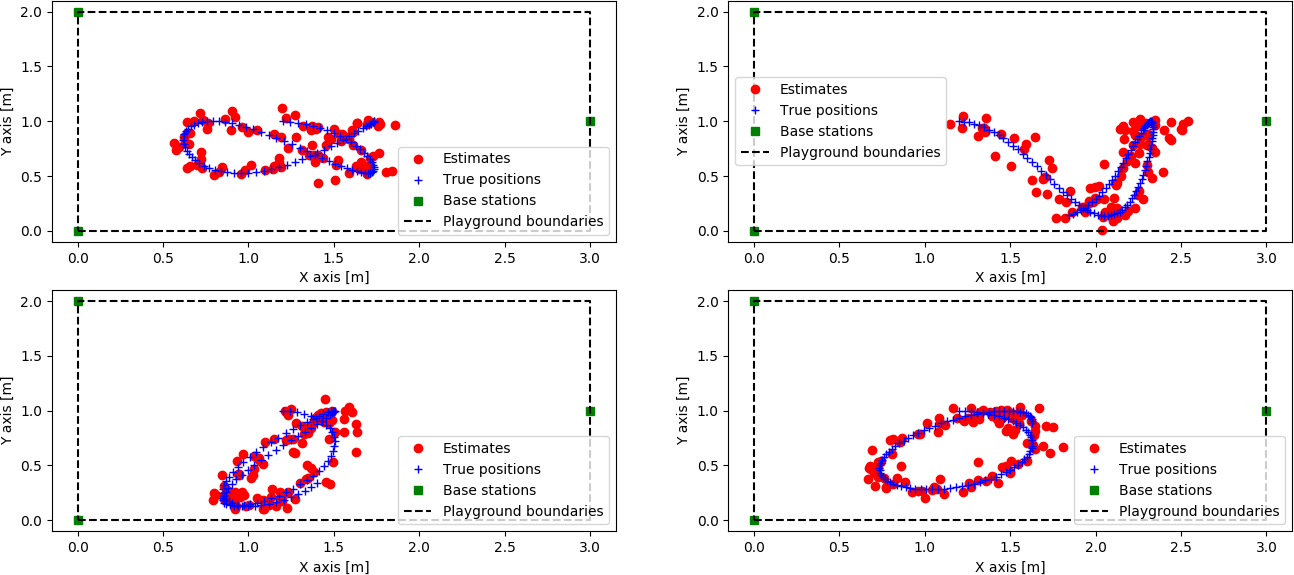
L’estimation se déroulant on peut ainsi calculer l'erreur entre cette dernière et les vraies positions, on notera cette dernière ainsi :$$\mathbf{\delta} = \hat{\mathbf{p}} - \underbrace{\mathbf{p}}_{\text{vraie position}}$$Le graphique ci-dessous comporte tous les points de ce terme d'erreur pour les quatre trajectoires ci dessous.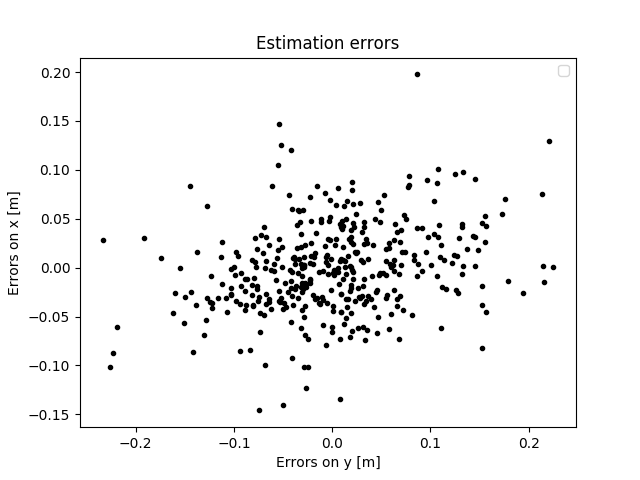
Au vu de la simplicité de l'algorithme, il n'est pas robuste aux bruits de mesure, et si on augmente trop le bruit additif sur les angles, le résultat ne se montre plus satisfaisant. Ainsi, il faut intégrer la cinématique du robot (ici on prend des "photographies robot à l'instant t" en supposant le robot fixe et disposant des trois angles en même temps) afin de lisser l'estimé de trajectoire.

Méthodes par moindres carrés et filtrage de Kalman

Comme support de ceci, je ne donne pas de version HTML lisible sur navigateur mais... des slides Beamer ce qui est mieux pour les yeux! Je précise que ces supports sont donnés pour la formation qui aura lieu en janvier 2020 au Club Robotique de l'École Centrale de Marseille... E-Gab!

• Présentation donnée à l'École Centrale de Marseille [PDF]
• Codes-compagnons pour cette formation plus du bonus! In English in the text. [Répertoire Gitlab]
  
• Bibliothèque en C pour une impémentation sur micro-contôleur d'un EKF (pas super, c'est moi qui l'ai codée, mais cela fonctionne). [Répertoire Gitlab]
  
• Motion planning (planification de trajectoire) en robotique (utile pour mieux comprendre la cinématique) [PDF]
  
• Page contenant mes travaux de recherche pour les plus téméraires.
  

Retour vers la page principale du site.

Haut de page